Understanding The Meaning Of Proportional

What Does Proportional Mean? When we talk about proportionality, we are referring to the relationship between two quantities. This means that as one quantity changes, the other changes in a predictable and consistent manner. In other words, when one variable increases or decreases, the other variable also increases or decreases in a corresponding way. Proportional relationships can be found in various aspects of our daily lives, from simple mathematical equations to more complex real-world scenarios.

Understanding the concept of proportionality is essential in various fields such as mathematics, economics, and science. It allows us to make predictions, analyze data, and make informed decisions based on the relationship between different variables. By grasping the meaning of proportional, we can gain a deeper understanding of how different quantities interact with each other and how changes in one quantity can affect another.

Proportional relationships play a crucial role in many areas of study and are fundamental to comprehending various phenomena in the world around us. Whether it's understanding the relationship between speed and distance, or the connection between input and output in a business context, the concept of proportionality is an integral part of our daily lives.

What are the Characteristics of Proportional Relationships?

A proportional relationship between two quantities has several key characteristics that distinguish it from other types of relationships. Understanding these characteristics can help us identify and analyze proportional relationships in different contexts. Some of the main characteristics of proportional relationships include:

Direct Variation

One of the primary characteristics of a proportional relationship is direct variation. This means that as one quantity increases, the other quantity also increases, and as one quantity decreases, the other quantity decreases. The relationship between the two quantities maintains a consistent ratio, leading to a straight-line graph when plotted on a coordinate plane.

Constant of Proportionality

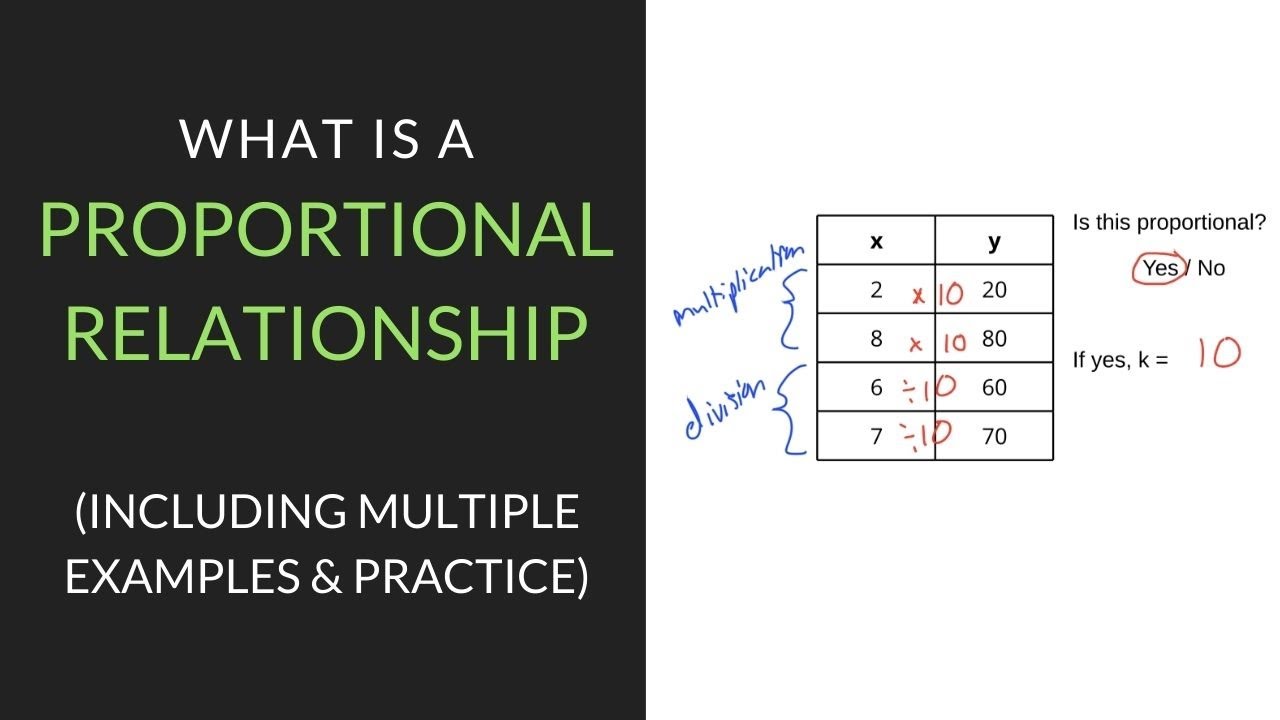
Another important characteristic of proportional relationships is the constant of proportionality. This constant, often denoted by the letter k, represents the ratio between the two quantities in the relationship. It is a fixed value that remains the same throughout the relationship, regardless of the specific values of the quantities involved.

Graphical Representation

Proportional relationships can be visually represented through graphs, where the points plotted form a straight line that passes through the origin (0,0). This graphical representation helps us visualize the relationship between the two quantities and understand how they change in relation to each other.

How Do You Identify Proportional Relationships?

Identifying proportional relationships involves recognizing the key characteristics and patterns that define such relationships. There are several methods and approaches that can be used to identify proportional relationships in different contexts. Some of the common ways to identify proportional relationships include:

Graphical Analysis

One way to identify a proportional relationship is by graphing the data and observing the pattern formed. If the plotted points form a straight line that passes through the origin, it indicates a proportional relationship between the two quantities. This visual representation can help in quickly identifying proportional relationships.

Calculation of Ratios

Calculating the ratios between the values of the two quantities can also help in identifying proportional relationships. If the ratios remain constant for different sets of values, it indicates a proportional relationship. By comparing the ratios, one can determine whether the relationship between the quantities is proportional or not.

Using the Constant of Proportionality

Another method of identifying proportional relationships involves using the constant of proportionality. By calculating the constant of proportionality from the given data, one can determine whether the relationship between the quantities is proportional or not. If the constant remains the same for different sets of values, it indicates a proportional relationship.

Why is Understanding Proportional Relationships Important?

Understanding proportional relationships is crucial as it has practical applications in various fields and disciplines. Whether it's in mathematics, science, finance, or everyday decision-making, the concept of proportionality plays a significant role. Some of the reasons why understanding proportional relationships is important include:

Real-World Applications

Proportional relationships have numerous real-world applications, from calculating unit prices at the grocery store to analyzing the relationship between time and distance in travel. Understanding proportionality allows us to make sense of these real-world scenarios and make informed decisions based on the relationship between different quantities.

Data Analysis and Interpretation

In fields such as economics and science, understanding proportional relationships is essential for data analysis and interpretation. It allows researchers and analysts to identify trends, make predictions, and draw meaningful conclusions based on the relationship between variables. Proportionality provides a framework for analyzing data and understanding the connections between different factors.

Problem-Solving and Decision Making

Proportional relationships play a vital role in problem-solving and decision-making processes. Whether it's in business, engineering, or everyday life, understanding proportionality helps in making calculations, solving problems, and making decisions based on the relationship between different quantities. It provides a structured approach to analyzing and solving problems involving varying quantities.

How Can Proportional Relationships Be Utilized in Different Fields?

Proportional relationships have diverse applications across various fields and disciplines. From mathematics to physics, finance to engineering, the concept of proportionality is utilized in different ways to analyze data, make predictions, and solve problems. Some of the ways in which proportional relationships are utilized in different fields include:

Mathematics and Science

In mathematics and science, proportional relationships are used to analyze data, make predictions, and understand the connections between different variables. Whether it's in physics, chemistry, or biology, proportionality provides a framework for interpreting data and drawing conclusions based on the relationship between quantities.

Finance and Economics

In finance and economics, proportional relationships play a crucial role in analyzing trends, making financial projections, and understanding the impact of various factors on economic outcomes. Whether it's calculating interest rates, analyzing market trends, or understanding the relationship between supply and demand, proportionality is essential in financial and economic analysis.

Engineering and Technology

In engineering and technology, proportional relationships are utilized in various calculations, design processes, and problem-solving scenarios. Whether it's in designing mechanical systems, analyzing electrical circuits, or optimizing technological processes, understanding proportionality is essential for ensuring the efficiency and effectiveness of engineering solutions.

Conclusion

In conclusion, understanding the meaning of proportional relationships is crucial for comprehending the connections between different quantities and their interactions. Whether it's in mathematics, science, finance, or everyday decision-making, the concept of proportionality provides a framework for analyzing data, making predictions, and solving problems based on the relationship between variables. By recognizing the characteristics of proportional relationships and their practical applications, we can gain a deeper understanding of the world around us and make informed decisions based on the principles of proportionality.